Distance Estimation
To accurately determine a diagonal distance when you know the distance of two perpendicular edges, you can apply the Pythagorean theorum. Given perpendicular edges with lengths a and b, just square a, square b, and take the square root to get the final length.
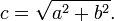
(Image from the "Pythagorean
theorem" article at Wikipedia.)
It turns out that calculating this is moderately common for tabletop games played on a grid. However, people may not have a calculator handy, so there are simpler solutions designed to give a good enough approximation. I was curious how accurate these approximations were.
Percentage error for various estimation systems:
| Max | Average | Median | Mode | |
|---|---|---|---|---|
| 1.5 long diagonals | 11.80% | 8.93% | 9.71% | 10.00% |
| 1-then-2 | 29.29% | 8.51% | 9.27% | 9.32% |
| Long only | 29.29% | 11.98% | 10.65% | 10.56% |
| New York blocks | 41.42% | 29.85% | 34.25% | 34.16% |
These were calculated by considering every possibility for integer distances from 1 through 100 for each of the two orthogonal edges.
Actual Calculated using the Pythagorean theorum.
1.5 long diagonals Add the length of the longer orthogonal edge to half of the length of the other orthogonal edge. This is common for games built on a grid; players are told that diagonal movement is measured as 1.5 units. Very accurate on very shallow angles, and accurate to about 6% near 45 degrees. Between those angles the error spikes up to 12%, with the spike being wider as the distances increase. This measurement only works if you include the half-unit that may be included. If you round off, you'll end up with 1-then-2.
1-then-2 This is a minor tweak to 1.5 long diagonals, and was used in 3rd edition Dungeons & Dragons. When moving diagonally on the grid, the first diagonal step is measured as 1 unit, the next 2 units, the next 1 unit, the next 2 units, and so on. It identical to 1.5 long diagonals, rounding the result down. down. The 29% error is a fluke; the single location 1,1 is wildly wrong because it's been rounded from 1.41 to 1. Beyond that, the stair step function causes the error to bounce up and down, sometimes being more accurate than 1.5 long diagonals, and sometimes less.
Long only Use the length of longest orthogonal edge. This is common for games built on a grid; players are told that they may move diagonally, but measure it as a single unit. 4th edition Dungeons & Dragons moved to this system. The closer you get to 45 degrees, the error increases, peaking around 29%.
New York Block Add the length of the two orthogonal edges together. Again, this is common for games built on a grid; players are told that only movement along the two orthogonal directions are allowed. The closer you get to 45 degrees, the error increases, eventually peaking around 41%. The longer the distances, the more quickly the error approaches 41%

